$\Delta[2150][+1]$ Two Body Decay Vertices(58)

There are 58 vertices in this part

Vertex 59: $\gamma^{0}_{\beta }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- N[1990]^+({p_1})~$

$$\begin{eqnarray*} &V_{59}=g~(- \sqrt{{p_1}^2}{p_3}_\nu {p_3}_\alpha g_{\mu ,\be... ...f_{891}+\gamma_\beta {p_3}_\mu {p_3}_\nu {p_3}_\alpha f_{892}i) \end{eqnarray*}$$

Vertex 60: $N[1990]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{\beta }~( {p_3})~$

$$\begin{eqnarray*} &V_{60}=g~( \sqrt{{p_1}^2}{p_3}_\nu {p_3}_\alpha g_{\mu ,\bet... ...f_{891}+\gamma_\beta {p_3}_\mu {p_3}_\nu {p_3}_\alpha f_{892}i) \end{eqnarray*}$$

Vertex 61: $\gamma^{0}_{\beta }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- \Delta[1950][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{61}=g~(- \sqrt{{p_1}^2}{p_3}_\nu {p_3}_\alpha g_{\mu ,\be... ...f_{864}+\gamma_\beta {p_3}_\mu {p_3}_\nu {p_3}_\alpha f_{865}i) \end{eqnarray*}$$

Vertex 62: $\Delta[1950][+1]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{ \beta }~({p_3})~$

$$\begin{eqnarray*} &V_{62}=g~( \sqrt{{p_1}^2}{p_3}_\nu {p_3}_\alpha g_{\mu ,\bet... ...f_{864}+\gamma_\beta {p_3}_\mu {p_3}_\nu {p_3}_\alpha f_{865}i) \end{eqnarray*}$$

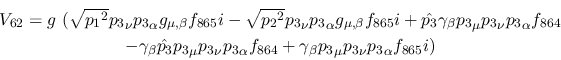
Vertex 63: $\gamma^{0}_{\alpha }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~ -N[1675]^+({p_1})~$

$$\begin{eqnarray*} &V_{63}=g~( \sqrt{{p_1}^2}{p_3}_\nu g_{\mu ,\alpha }f_{608}i-... ...3}_\nu f_{607} \\ &- \gamma_\alpha {p_3}_\mu {p_3}_\nu f_{608}i) \end{eqnarray*}$$

Vertex 64: $N[1675]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{\alpha }~( {p_3})~$

$$\begin{eqnarray*} &V_{64}=g~( \sqrt{{p_1}^2}{p_3}_\nu g_{\mu ,\alpha }f_{608}i-... ...3}_\nu f_{607} \\ &+ \gamma_\alpha {p_3}_\mu {p_3}_\nu f_{608}i) \end{eqnarray*}$$

Vertex 65: $\gamma^{0}_{\alpha }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~ -N[1680]^+({p_1})~$

$$\begin{eqnarray*} &V_{65}=g~(-\gamma_5{\hat {p_3}}\gamma_\alpha {p_3}_\mu {p_3}... ...\\ &- \sqrt{{p_2}^2}\gamma_5{p_3}_\nu g_{\mu ,\alpha } f_{580}i) \end{eqnarray*}$$

Vertex 66: $N[1680]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{\alpha }~( {p_3})~$

$$\begin{eqnarray*} &V_{66}=g~(\gamma_5{\hat {p_3}}\gamma_\alpha {p_3}_\mu {p_3}_... ...\\ &+ \sqrt{{p_2}^2}\gamma_5{p_3}_\nu g_{\mu ,\alpha } f_{580}i) \end{eqnarray*}$$

Vertex 67: $\gamma^{0}_{\alpha }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~ -N[2000]^+({p_1})~$

$$\begin{eqnarray*} &V_{67}=g~(-\gamma_5{\hat {p_3}}\gamma_\alpha {p_3}_\mu {p_3}... ...\\ &- \sqrt{{p_2}^2}\gamma_5{p_3}_\nu g_{\mu ,\alpha } f_{553}i) \end{eqnarray*}$$

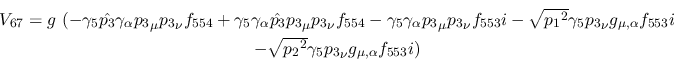
Vertex 68: $N[2000]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{\alpha }~( {p_3})~$

$$\begin{eqnarray*} &V_{68}=g~(\gamma_5{\hat {p_3}}\gamma_\alpha {p_3}_\mu {p_3}_... ...\\ &+ \sqrt{{p_2}^2}\gamma_5{p_3}_\nu g_{\mu ,\alpha } f_{553}i) \end{eqnarray*}$$

Vertex 69: $\gamma^{0}_{\alpha }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~ -\Delta[1905][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{69}=g~(-\gamma_5{\hat {p_3}}\gamma_\alpha {p_3}_\mu {p_3}... ...\\ &- \sqrt{{p_2}^2}\gamma_5{p_3}_\nu g_{\mu ,\alpha } f_{526}i) \end{eqnarray*}$$

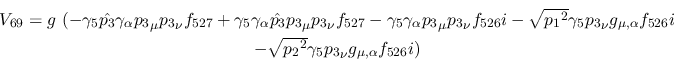
Vertex 70: $\Delta[1905][+1]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{ \alpha }~({p_3})~$

$$\begin{eqnarray*} &V_{70}=g~(\gamma_5{\hat {p_3}}\gamma_\alpha {p_3}_\mu {p_3}_... ...\\ &+ \sqrt{{p_2}^2}\gamma_5{p_3}_\nu g_{\mu ,\alpha } f_{526}i) \end{eqnarray*}$$

Vertex 71: $\gamma^{0}_{\alpha }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~ -\Delta[1930][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{71}=g~( \sqrt{{p_1}^2}{p_3}_\nu g_{\mu ,\alpha }f_{500}i-... ...3}_\nu f_{499} \\ &- \gamma_\alpha {p_3}_\mu {p_3}_\nu f_{500}i) \end{eqnarray*}$$

Vertex 72: $\Delta[1930][+1]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{ \alpha }~({p_3})~$

$$\begin{eqnarray*} &V_{72}=g~( \sqrt{{p_1}^2}{p_3}_\nu g_{\mu ,\alpha }f_{500}i-... ...3}_\nu f_{499} \\ &+ \gamma_\alpha {p_3}_\mu {p_3}_\nu f_{500}i) \end{eqnarray*}$$

Vertex 73: $\gamma^{0}_{\alpha }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~ -\Delta[2000][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{73}=g~(-\gamma_5{\hat {p_3}}\gamma_\alpha {p_3}_\mu {p_3}... ...\\ &- \sqrt{{p_2}^2}\gamma_5{p_3}_\nu g_{\mu ,\alpha } f_{472}i) \end{eqnarray*}$$

Vertex 74: $\Delta[2000][+1]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{ \alpha }~({p_3})~$

$$\begin{eqnarray*} &V_{74}=g~(\gamma_5{\hat {p_3}}\gamma_\alpha {p_3}_\mu {p_3}_... ...\\ &+ \sqrt{{p_2}^2}\gamma_5{p_3}_\nu g_{\mu ,\alpha } f_{472}i) \end{eqnarray*}$$

Vertex 75: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- N[1520]^+({p_1})~$

$$\begin{eqnarray*} &V_{75}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{430}-\... ...nu }f_{429}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{429}i) \end{eqnarray*}$$

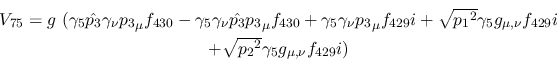
Vertex 76: $N[1520]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{\nu }~( {p_3})~$

$$\begin{eqnarray*} &V_{76}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{430}-\... ...nu }f_{429}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{429}i) \end{eqnarray*}$$

Vertex 77: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- N[1700]^+({p_1})~$

$$\begin{eqnarray*} &V_{77}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{403}-\... ...nu }f_{402}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{402}i) \end{eqnarray*}$$

Vertex 78: $N[1700]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{\nu }~( {p_3})~$

$$\begin{eqnarray*} &V_{78}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{403}-\... ...nu }f_{402}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{402}i) \end{eqnarray*}$$

Vertex 79: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- N[1720]^+({p_1})~$

$$\begin{eqnarray*} &V_{79}=g~(- \sqrt{{p_1}^2}g_{\mu ,\nu }f_{376}i+ \sqrt{{p_2}... ...nu {\hat {p_3}}{p_3}_ \mu f_{375}+\gamma_\nu {p_3}_\mu f_{376}i) \end{eqnarray*}$$

Vertex 80: $N[1720]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{\nu }~( {p_3})~$

$$\begin{eqnarray*} &V_{80}=g~( \sqrt{{p_1}^2}g_{\mu ,\nu }f_{376}i- \sqrt{{p_2}^... ...nu {\hat {p_3}}{p_3}_ \mu f_{375}+\gamma_\nu {p_3}_\mu f_{376}i) \end{eqnarray*}$$

Vertex 81: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- N[1900]^+({p_1})~$

$$\begin{eqnarray*} &V_{81}=g~(- \sqrt{{p_1}^2}g_{\mu ,\nu }f_{349}i+ \sqrt{{p_2}... ...nu {\hat {p_3}}{p_3}_ \mu f_{348}+\gamma_\nu {p_3}_\mu f_{349}i) \end{eqnarray*}$$

Vertex 82: $N[1900]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{\nu }~( {p_3})~$

$$\begin{eqnarray*} &V_{82}=g~( \sqrt{{p_1}^2}g_{\mu ,\nu }f_{349}i- \sqrt{{p_2}^... ...nu {\hat {p_3}}{p_3}_ \mu f_{348}+\gamma_\nu {p_3}_\mu f_{349}i) \end{eqnarray*}$$

Vertex 83: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- N[2080]^+({p_1})~$

$$\begin{eqnarray*} &V_{83}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{322}-\... ...nu }f_{321}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{321}i) \end{eqnarray*}$$

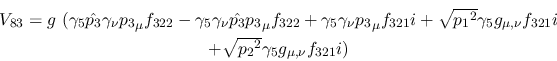
Vertex 84: $N[2080]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{\nu }~( {p_3})~$

$$\begin{eqnarray*} &V_{84}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{322}-\... ...nu }f_{321}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{321}i) \end{eqnarray*}$$

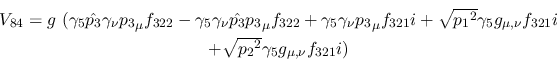
Vertex 85: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- \Delta[1232][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{85}=g~(- \sqrt{{p_1}^2}g_{\mu ,\nu }f_{277}i+ \sqrt{{p_2}... ...nu {\hat {p_3}}{p_3}_ \mu f_{276}+\gamma_\nu {p_3}_\mu f_{277}i) \end{eqnarray*}$$

Vertex 86: $\Delta[1232][+1]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{ \nu }~({p_3})~$

$$\begin{eqnarray*} &V_{86}=g~( \sqrt{{p_1}^2}g_{\mu ,\nu }f_{277}i- \sqrt{{p_2}^... ...nu {\hat {p_3}}{p_3}_ \mu f_{276}+\gamma_\nu {p_3}_\mu f_{277}i) \end{eqnarray*}$$

Vertex 87: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- \Delta[1600][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{87}=g~(- \sqrt{{p_1}^2}g_{\mu ,\nu }f_{247}i+ \sqrt{{p_2}... ...nu {\hat {p_3}}{p_3}_ \mu f_{246}+\gamma_\nu {p_3}_\mu f_{247}i) \end{eqnarray*}$$

Vertex 88: $\Delta[1600][+1]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{ \nu }~({p_3})~$

$$\begin{eqnarray*} &V_{88}=g~( \sqrt{{p_1}^2}g_{\mu ,\nu }f_{247}i- \sqrt{{p_2}^... ...nu {\hat {p_3}}{p_3}_ \mu f_{246}+\gamma_\nu {p_3}_\mu f_{247}i) \end{eqnarray*}$$

Vertex 89: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- \Delta[1700][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{89}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{220}-\... ...nu }f_{219}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{219}i) \end{eqnarray*}$$

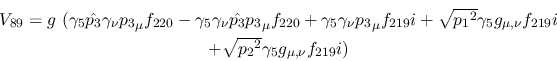
Vertex 90: $\Delta[1700][+1]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{ \nu }~({p_3})~$

$$\begin{eqnarray*} &V_{90}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{220}-\... ...nu }f_{219}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{219}i) \end{eqnarray*}$$

Vertex 91: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- \Delta[1920][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{91}=g~(- \sqrt{{p_1}^2}g_{\mu ,\nu }f_{193}i+ \sqrt{{p_2}... ...nu {\hat {p_3}}{p_3}_ \mu f_{192}+\gamma_\nu {p_3}_\mu f_{193}i) \end{eqnarray*}$$

Vertex 92: $\Delta[1920][+1]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{ \nu }~({p_3})~$

$$\begin{eqnarray*} &V_{92}=g~( \sqrt{{p_1}^2}g_{\mu ,\nu }f_{193}i- \sqrt{{p_2}^... ...nu {\hat {p_3}}{p_3}_ \mu f_{192}+\gamma_\nu {p_3}_\mu f_{193}i) \end{eqnarray*}$$

Vertex 93: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[2150][+1]}({p_2})~- \Delta[1940][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{93}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{166}-\... ...nu }f_{165}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{165}i) \end{eqnarray*}$$

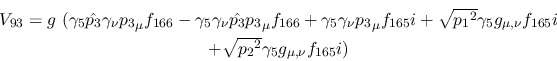
Vertex 94: $\Delta[1940][+1]^-({p_1})~-\Delta[2150][+1]({p_2})~-\gamma^{0}_{ \nu }~({p_3})~$

$$\begin{eqnarray*} &V_{94}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{166}-\... ...nu }f_{165}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{165}i) \end{eqnarray*}$$

Vertex 95: $\gamma^{0}_{\mu }~({p_3})~-\overline{P}({p_2})~-\Delta[2150][+1]( {p_1})~$

$$\begin{eqnarray*} &V_{95}=f_{59}g~(-\gamma_5{\hat {p_3}}\gamma_\mu +\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 96: $\overline{\Delta[2150][+1]}({p_1})~-P({p_2})~-\gamma^{0}_{\mu }~( {p_3})~$

$$\begin{eqnarray*} &V_{96}=f_{59}g~(\gamma_5{\hat {p_3}}\gamma_\mu -\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 97: $\gamma^{0}_{\mu }~({p_3})~-\overline{N[1440]}({p_2})~- \Delta[2150][+1]({p_1})~$

$$\begin{eqnarray*} &V_{97}=f_{56}g~(-\gamma_5{\hat {p_3}}\gamma_\mu +\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 98: $\overline{\Delta[2150][+1]}({p_1})~-N[1440]({p_2})~-\gamma^{0}_{ \mu }~({p_3})~$

$$\begin{eqnarray*} &V_{98}=f_{56}g~(\gamma_5{\hat {p_3}}\gamma_\mu -\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 99: $\gamma^{0}_{\mu }~({p_3})~-\overline{N[1535]}({p_2})~- \Delta[2150][+1]({p_1})~$

$$\begin{eqnarray*} &V_{99}=f_{55}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 100: $\overline{\Delta[2150][+1]}({p_1})~-N[1535]({p_2})~-\gamma^{0}_{ \mu }~({p_3})~$

$$\begin{eqnarray*} &V_{100}=f_{55}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 101: $\gamma^{0}_{\mu }~({p_3})~-\overline{N[1650]}({p_2})~- \Delta[2150][+1]({p_1})~$

$$\begin{eqnarray*} &V_{101}=f_{54}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 102: $\overline{\Delta[2150][+1]}({p_1})~-N[1650]({p_2})~-\gamma^{0}_{ \mu }~({p_3})~$

$$\begin{eqnarray*} &V_{102}=f_{54}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 103: $\gamma^{0}_{\mu }~({p_3})~-\overline{N[1710]}({p_2})~- \Delta[2150][+1]({p_1})~$

$$\begin{eqnarray*} &V_{103}=f_{53}g~(-\gamma_5{\hat {p_3}}\gamma_\mu +\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 104: $\overline{\Delta[2150][+1]}({p_1})~-N[1710]({p_2})~-\gamma^{0}_{ \mu }~({p_3})~$

$$\begin{eqnarray*} &V_{104}=f_{53}g~(\gamma_5{\hat {p_3}}\gamma_\mu -\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 105: $\gamma^{0}_{\mu }~({p_3})~-\overline{N[2090]}({p_2})~- \Delta[2150][+1]({p_1})~$

$$\begin{eqnarray*} &V_{105}=f_{52}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 106: $\overline{\Delta[2150][+1]}({p_1})~-N[2090]({p_2})~-\gamma^{0}_{ \mu }~({p_3})~$

$$\begin{eqnarray*} &V_{106}=f_{52}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 107: $\gamma^{0}_{\mu }~({p_3})~-\overline{N[2100]}({p_2})~- \Delta[2150][+1]({p_1})~$

$$\begin{eqnarray*} &V_{107}=f_{51}g~(-\gamma_5{\hat {p_3}}\gamma_\mu +\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 108: $\overline{\Delta[2150][+1]}({p_1})~-N[2100]({p_2})~-\gamma^{0}_{ \mu }~({p_3})~$

$$\begin{eqnarray*} &V_{108}=f_{51}g~(\gamma_5{\hat {p_3}}\gamma_\mu -\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 109: $\gamma^{0}_{\mu }~({p_3})~-\overline{\Delta[1620][+1]}({p_2})~- \Delta[2150][+1]({p_1})~$

$$\begin{eqnarray*} &V_{109}=f_{50}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 110: $\overline{\Delta[2150][+1]}({p_1})~-\Delta[1620][+1]({p_2})~- \gamma^{0}_{\mu }~({p_3})~$

$$\begin{eqnarray*} &V_{110}=f_{50}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 111: $\gamma^{0}_{\mu }~({p_3})~-\overline{\Delta[1750][+1]}({p_2})~- \Delta[2150][+1]({p_1})~$

$$\begin{eqnarray*} &V_{111}=f_{49}g~(-\gamma_5{\hat {p_3}}\gamma_\mu +\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 112: $\overline{\Delta[2150][+1]}({p_1})~-\Delta[1750][+1]({p_2})~- \gamma^{0}_{\mu }~({p_3})~$

$$\begin{eqnarray*} &V_{112}=f_{49}g~(\gamma_5{\hat {p_3}}\gamma_\mu -\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 113: $\gamma^{0}_{\mu }~({p_3})~-\overline{\Delta[1900][+1]}({p_2})~- \Delta[2150][+1]({p_1})~$

$$\begin{eqnarray*} &V_{113}=f_{48}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 114: $\overline{\Delta[2150][+1]}({p_1})~-\Delta[1900][+1]({p_2})~- \gamma^{0}_{\mu }~({p_3})~$

$$\begin{eqnarray*} &V_{114}=f_{48}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 115: $\gamma^{0}_{\mu }~({p_3})~-\overline{\Delta[1910][+1]}({p_2})~- \Delta[2150][+1]({p_1})~$

$$\begin{eqnarray*} &V_{115}=f_{47}g~(-\gamma_5{\hat {p_3}}\gamma_\mu +\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 116: $\overline{\Delta[2150][+1]}({p_1})~-\Delta[1910][+1]({p_2})~- \gamma^{0}_{\mu }~({p_3})~$

$$\begin{eqnarray*} &V_{116}=f_{47}g~(\gamma_5{\hat {p_3}}\gamma_\mu -\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$