$K_2[1580]^+$ Two Body Decay Vertices(18)

There are 18 vertices in this part

Vertex 19: $\gamma^{0}_{\beta }~({p_3})~-K^{*}[892]^-_{\alpha }~({p_2})~- K_2[1580]^+_{\mu ,\nu }~({p_1})~$

$$\begin{eqnarray*} &V_{19}={\displaystyle{gi \over 2}}~(-{p_1}^2{p_3}_\nu \epsil... ...25}-2g_{\nu ,\beta }\epsilon_{{p_1},{p_3},\mu , \alpha }f_{826}) \end{eqnarray*}$$

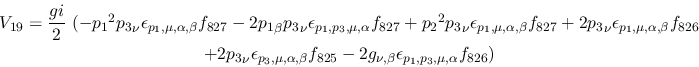
Vertex 20: $K_2[1580]^-_{\mu ,\nu }~({p_1})~-K^{*}[892]^+_{\alpha }~({p_2})~- \gamma^{0}_{\beta }~({p_3})~$

$$\begin{eqnarray*} &V_{20}={\displaystyle{gi \over 2}}~({p_1}^2{p_3}_\nu \epsilo... ...25}+2g_{\nu ,\beta }\epsilon_{{p_1},{p_3},\mu , \alpha }f_{826}) \end{eqnarray*}$$

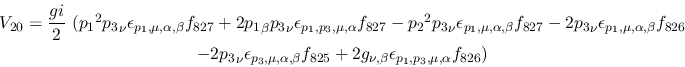
Vertex 21: $\gamma^{0}_{\beta }~({p_3})~-K_1[1270]^-_{\alpha }~({p_2})~- K_2[1580]^+_{\mu ,\nu }~({p_1})~$

$$\begin{eqnarray*} &V_{21}={\displaystyle{gi \over 2}}~(-{p_1}^2{p_3}_\nu {p_3}_... ...,\beta } f_{823}+2{p_3}_\nu {p_3}_\alpha g_{\mu ,\beta }f_{823}) \end{eqnarray*}$$

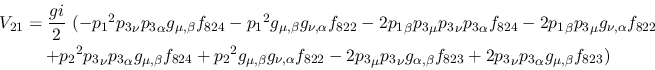
Vertex 22: $K_2[1580]^-_{\mu ,\nu }~({p_1})~-K_1[1270]^+_{\alpha }~({p_2})~- \gamma^{0}_{\beta }~({p_3})~$

$$\begin{eqnarray*} &V_{22}={\displaystyle{gi \over 2}}~({p_1}^2{p_3}_\nu {p_3}_\... ...,\beta } f_{823}-2{p_3}_\nu {p_3}_\alpha g_{\mu ,\beta }f_{823}) \end{eqnarray*}$$

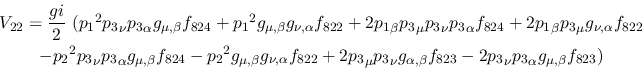
Vertex 23: $\gamma^{0}_{\beta }~({p_3})~-K_1[1400]^-_{\alpha }~({p_2})~- K_2[1580]^+_{\mu ,\nu }~({p_1})~$

$$\begin{eqnarray*} &V_{23}={\displaystyle{gi \over 2}}~(-{p_1}^2{p_3}_\nu {p_3}_... ...,\beta } f_{820}+2{p_3}_\nu {p_3}_\alpha g_{\mu ,\beta }f_{820}) \end{eqnarray*}$$

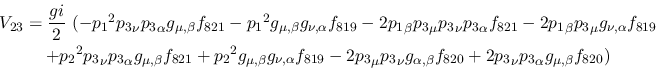
Vertex 24: $K_2[1580]^-_{\mu ,\nu }~({p_1})~-K_1[1400]^+_{\alpha }~({p_2})~- \gamma^{0}_{\beta }~({p_3})~$

$$\begin{eqnarray*} &V_{24}={\displaystyle{gi \over 2}}~({p_1}^2{p_3}_\nu {p_3}_\... ...,\beta } f_{820}-2{p_3}_\nu {p_3}_\alpha g_{\mu ,\beta }f_{820}) \end{eqnarray*}$$

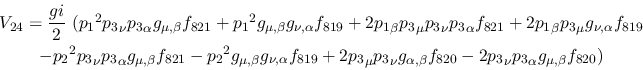
Vertex 25: $\gamma^{0}_{\beta }~({p_3})~-K^{*}[1410]^-_{\alpha }~({p_2})~- K_2[1580]^+_{\mu ,\nu }~({p_1})~$

$$\begin{eqnarray*} &V_{25}={\displaystyle{gi \over 2}}~(-{p_1}^2{p_3}_\nu \epsil... ...16}-2g_{\nu ,\beta }\epsilon_{{p_1},{p_3},\mu , \alpha }f_{817}) \end{eqnarray*}$$

Vertex 26: $K_2[1580]^-_{\mu ,\nu }~({p_1})~-K^{*}[1410]^+_{\alpha }~({p_2})~ -\gamma^{0}_{\beta }~({p_3})~$

$$\begin{eqnarray*} &V_{26}={\displaystyle{gi \over 2}}~({p_1}^2{p_3}_\nu \epsilo... ...16}+2g_{\nu ,\beta }\epsilon_{{p_1},{p_3},\mu , \alpha }f_{817}) \end{eqnarray*}$$

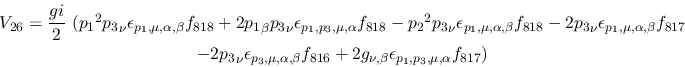
Vertex 27: $K^-({p_3})~-\gamma^{0}_{\alpha }~({p_2})~-K_2[1580]^+_{\mu ,\nu }~({p_1})~$

$$\begin{eqnarray*} &V_{27}={\displaystyle{f_{611}g \over 2}}~(-{p_1}^2{p_2}_\nu ... ...}_\alpha {p_2}_\mu {p_2}_\nu +{p_2}_\nu {p_3}^2g_{\mu ,\alpha }) \end{eqnarray*}$$

Vertex 28: $K_2[1580]^-_{\mu ,\nu }~({p_1})~-\gamma^{0}_{\alpha }~({p_2})~- K^+({p_3})~$

$$\begin{eqnarray*} &V_{28}={\displaystyle{f_{611}g \over 2}}~({p_1}^2{p_2}_\nu g... ...}_\alpha {p_2}_\mu {p_2}_\nu -{p_2}_\nu {p_3}^2g_{\mu ,\alpha }) \end{eqnarray*}$$

Vertex 29: $K[1460]^-({p_3})~-\gamma^{0}_{\alpha }~({p_2})~-K_2[1580]^+_{\mu ,\nu }~({p_1})~$

$$\begin{eqnarray*} &V_{29}={\displaystyle{f_{610}g \over 2}}~(-{p_1}^2{p_2}_\nu ... ...}_\alpha {p_2}_\mu {p_2}_\nu +{p_2}_\nu {p_3}^2g_{\mu ,\alpha }) \end{eqnarray*}$$

Vertex 30: $K_2[1580]^-_{\mu ,\nu }~({p_1})~-\gamma^{0}_{\alpha }~({p_2})~- K[1460]^+({p_3})~$

$$\begin{eqnarray*} &V_{30}={\displaystyle{f_{610}g \over 2}}~({p_1}^2{p_2}_\nu g... ...}_\alpha {p_2}_\mu {p_2}_\nu -{p_2}_\nu {p_3}^2g_{\mu ,\alpha }) \end{eqnarray*}$$

Vertex 31: $K^-({p_3})~-\omega[782]^{0}_{\alpha }~({p_2})~-K_2[1580]^+_{\mu , \nu }~({p_1})~$

$$\begin{eqnarray*} &V_{31}=-g~({p_1}_\alpha {p_2}_\mu {p_2}_\nu f_{608}+{p_2}_\mu g_{\nu ,\alpha }f_{607}) \end{eqnarray*}$$

Vertex 32: $K_2[1580]^-_{\mu ,\nu }~({p_1})~-\omega[782]^{0}_{\alpha }~({p_2} )~-K^+({p_3})~$

$$\begin{eqnarray*} &V_{32}=g~({p_1}_\alpha {p_2}_\mu {p_2}_\nu f_{608}+{p_2}_\mu g_{\nu ,\alpha } f_{607}) \end{eqnarray*}$$

Vertex 33: $K^-({p_3})~-\phi[1020]^{0}_{\alpha }~({p_2})~-K_2[1580]^+_{\mu , \nu }~({p_1})~$

$$\begin{eqnarray*} &V_{33}=-g~({p_1}_\alpha {p_2}_\mu {p_2}_\nu f_{606}+{p_2}_\mu g_{\nu ,\alpha }f_{605}) \end{eqnarray*}$$

Vertex 34: $K_2[1580]^-_{\mu ,\nu }~({p_1})~-\phi[1020]^{0}_{\alpha }~({p_2} )~-K^+({p_3})~$

$$\begin{eqnarray*} &V_{34}=g~({p_1}_\alpha {p_2}_\mu {p_2}_\nu f_{606}+{p_2}_\mu g_{\nu ,\alpha } f_{605}) \end{eqnarray*}$$

Vertex 35: $\eta^{0}({p_3})~-K^{*}[892]^-_{\alpha }~({p_2})~-K_2[1580]^+_{ \mu ,\nu }~({p_1})~$

$$\begin{eqnarray*} &V_{35}=gi~({p_1}_\alpha {p_2}_\mu {p_2}_\nu f_{604}+{p_2}_\mu g_{\nu ,\alpha }f_{603}) \end{eqnarray*}$$

Vertex 36: $K_2[1580]^-_{\mu ,\nu }~({p_1})~-K^{*}[892]^+_{\alpha }~({p_2})~- \eta^{0}({p_3})~$

$$\begin{eqnarray*} &V_{36}=gi~({p_1}_\alpha {p_2}_\mu {p_2}_\nu f_{604}+{p_2}_\mu g_{\nu ,\alpha }f_{603}) \end{eqnarray*}$$