$f^{'}_2[1525]^{0}$ Two Body Decay Vertices(11)

There are 11 vertices in this part

Vertex 12: $\pi^-({p_3})~-a_2[1320]^+_{\alpha ,\beta }~({p_2})~- f^{'}_2[1525]^{0}_{\mu ,\nu }~({p_1})~$

$$\begin{eqnarray*} &V_{12}=-\epsilon_{{p_1},{p_2},\mu ,\alpha }g~({p_1}_\beta {p_2}_\nu f_{1582}+ g_{\nu ,\beta }f_{1581}) \end{eqnarray*}$$

Vertex 13: $f^{'}_2[1525]^{0}_{\mu ,\nu }~({p_1})~-a_2[1320]^-_{\alpha , \beta }~({p_2})~-\pi^+({p_3})~$

$$\begin{eqnarray*} &V_{13}=-\epsilon_{{p_1},{p_2},\mu ,\alpha }g~({p_1}_\beta {p_2}_\nu f_{1582}+ g_{\nu ,\beta }f_{1581}) \end{eqnarray*}$$

Vertex 14: $f^{'}_2[1525]^{0}_{\mu ,\nu }~({p_1})~-\omega[782]^{0}_{\alpha }~ ({p_2})~-\gamma^{0}_{\beta }~({p_3})~$

$$\begin{eqnarray*} &V_{14}={\displaystyle{g \over 2}}~({p_1}^2{p_3}_\nu {p_3}_\a... ...beta } f_{1291}-2{p_3}_\nu {p_3}_\alpha g_{\mu ,\beta }f_{1291}) \end{eqnarray*}$$

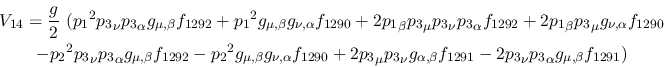
Vertex 15: $f^{'}_2[1525]^{0}_{\mu ,\nu }~({p_1})~-\phi[1020]^{0}_{\alpha }~( {p_2})~-\gamma^{0}_{\beta }~({p_3})~$

$$\begin{eqnarray*} &V_{15}={\displaystyle{g \over 2}}~({p_1}^2{p_3}_\nu {p_3}_\a... ...beta } f_{1288}-2{p_3}_\nu {p_3}_\alpha g_{\mu ,\beta }f_{1288}) \end{eqnarray*}$$

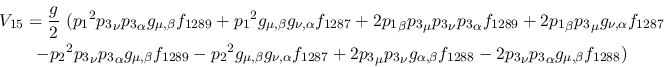
Vertex 16: $f^{'}_2[1525]^{0}_{\mu ,\nu }~({p_1})~-h_1[1170]^{0}_{\alpha }~( {p_2})~-\gamma^{0}_{\beta }~({p_3})~$

$$\begin{eqnarray*} &V_{16}={\displaystyle{g \over 2}}~({p_1}^2{p_3}_\nu \epsilon... ...4}+2g_{\nu ,\beta }\epsilon_{{p_1}, {p_3},\mu ,\alpha }f_{1285}) \end{eqnarray*}$$

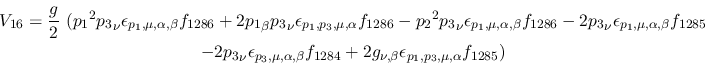
Vertex 17: $f^{'}_2[1525]^{0}_{\mu ,\nu }~({p_1})~-h_1[1380]^{0}_{\alpha }~( {p_2})~-\gamma^{0}_{\beta }~({p_3})~$

$$\begin{eqnarray*} &V_{17}={\displaystyle{g \over 2}}~({p_1}^2{p_3}_\nu \epsilon... ...1}+2g_{\nu ,\beta }\epsilon_{{p_1}, {p_3},\mu ,\alpha }f_{1282}) \end{eqnarray*}$$

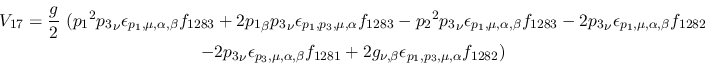
Vertex 18: $f^{'}_2[1525]^{0}_{\mu ,\nu }~({p_1})~-\omega[1420]^{0}_{\alpha }~({p_2})~-\gamma^{0}_{\beta }~({p_3})~$

$$\begin{eqnarray*} &V_{18}={\displaystyle{g \over 2}}~({p_1}^2{p_3}_\nu {p_3}_\a... ...beta } f_{1279}-2{p_3}_\nu {p_3}_\alpha g_{\mu ,\beta }f_{1279}) \end{eqnarray*}$$

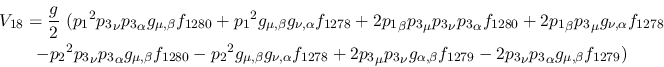
Vertex 19: $\pi^-({p_3})~-\pi_1[1400]^+_{\alpha }~({p_2})~-f^{'}_2[1525]^{0} _{\mu ,\nu }~({p_1})~$

$$\begin{eqnarray*} &V_{19}=-\epsilon_{{p_1},{p_2},\mu ,\alpha }f_{542}gi~{p_2}_\nu \end{eqnarray*}$$

Vertex 20: $f^{'}_2[1525]^{0}_{\mu ,\nu }~({p_1})~-\pi_1[1400]^-_{\alpha }~( {p_2})~-\pi^+({p_3})~$

$$\begin{eqnarray*} &V_{20}=-\epsilon_{{p_1},{p_2},\mu ,\alpha }f_{542}gi~{p_2}_\nu \end{eqnarray*}$$

Vertex 21: $f^{'}_2[1525]^{0}_{\mu ,\nu }~({p_1})~-\pi^-({p_2})~-\pi^+({p_3} )~$

$$\begin{eqnarray*} &V_{21}=f_{418}g~{p_2}_\mu {p_2}_\nu \end{eqnarray*}$$

Vertex 22: $f^{'}_2[1525]^{0}_{\mu ,\nu }~({p_1})~-f_0[600]^{0}({p_2})~- f_0[600]^{0}({p_3})~$

$$\begin{eqnarray*} &V_{22}=f_{417}g~{p_2}_\mu {p_2}_\nu \end{eqnarray*}$$