$\Delta[1750][+1]$ Two Body Decay Vertices(40)

There are 40 vertices in this part

Vertex 41: $\gamma^{0}_{\alpha }~({p_3})~-\overline{\Delta[1750][+1]}({p_2})~ -N[1675]^+({p_1})~$

$$\begin{eqnarray*} &V_{41}=g~(-\gamma_5{\hat {p_3}}\gamma_\alpha {p_3}_\mu {p_3}... ...\\ &- \sqrt{{p_2}^2}\gamma_5{p_3}_\nu g_{\mu ,\alpha } f_{596}i) \end{eqnarray*}$$

Vertex 42: $N[1675]^-({p_1})~-\Delta[1750][+1]({p_2})~-\gamma^{0}_{\alpha }~( {p_3})~$

$$\begin{eqnarray*} &V_{42}=g~(\gamma_5{\hat {p_3}}\gamma_\alpha {p_3}_\mu {p_3}_... ...\\ &+ \sqrt{{p_2}^2}\gamma_5{p_3}_\nu g_{\mu ,\alpha } f_{596}i) \end{eqnarray*}$$

Vertex 43: $\gamma^{0}_{\alpha }~({p_3})~-\overline{\Delta[1750][+1]}({p_2})~ -N[1680]^+({p_1})~$

$$\begin{eqnarray*} &V_{43}=g~( \sqrt{{p_1}^2}{p_3}_\nu g_{\mu ,\alpha }f_{579}i-... ...3}_\nu f_{578} \\ &- \gamma_\alpha {p_3}_\mu {p_3}_\nu f_{579}i) \end{eqnarray*}$$

Vertex 44: $N[1680]^-({p_1})~-\Delta[1750][+1]({p_2})~-\gamma^{0}_{\alpha }~( {p_3})~$

$$\begin{eqnarray*} &V_{44}=g~( \sqrt{{p_1}^2}{p_3}_\nu g_{\mu ,\alpha }f_{579}i-... ...3}_\nu f_{578} \\ &+ \gamma_\alpha {p_3}_\mu {p_3}_\nu f_{579}i) \end{eqnarray*}$$

Vertex 45: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[1750][+1]}({p_2})~- N[1520]^+({p_1})~$

$$\begin{eqnarray*} &V_{45}=g~(- \sqrt{{p_1}^2}g_{\mu ,\nu }f_{401}i+ \sqrt{{p_2}... ...nu {\hat {p_3}}{p_3}_ \mu f_{400}+\gamma_\nu {p_3}_\mu f_{401}i) \end{eqnarray*}$$

Vertex 46: $N[1520]^-({p_1})~-\Delta[1750][+1]({p_2})~-\gamma^{0}_{\nu }~( {p_3})~$

$$\begin{eqnarray*} &V_{46}=g~( \sqrt{{p_1}^2}g_{\mu ,\nu }f_{401}i- \sqrt{{p_2}^... ...nu {\hat {p_3}}{p_3}_ \mu f_{400}+\gamma_\nu {p_3}_\mu f_{401}i) \end{eqnarray*}$$

Vertex 47: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[1750][+1]}({p_2})~- N[1700]^+({p_1})~$

$$\begin{eqnarray*} &V_{47}=g~(- \sqrt{{p_1}^2}g_{\mu ,\nu }f_{383}i+ \sqrt{{p_2}... ...nu {\hat {p_3}}{p_3}_ \mu f_{382}+\gamma_\nu {p_3}_\mu f_{383}i) \end{eqnarray*}$$

Vertex 48: $N[1700]^-({p_1})~-\Delta[1750][+1]({p_2})~-\gamma^{0}_{\nu }~( {p_3})~$

$$\begin{eqnarray*} &V_{48}=g~( \sqrt{{p_1}^2}g_{\mu ,\nu }f_{383}i- \sqrt{{p_2}^... ...nu {\hat {p_3}}{p_3}_ \mu f_{382}+\gamma_\nu {p_3}_\mu f_{383}i) \end{eqnarray*}$$

Vertex 49: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[1750][+1]}({p_2})~- N[1720]^+({p_1})~$

$$\begin{eqnarray*} &V_{49}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{365}-\... ...nu }f_{364}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{364}i) \end{eqnarray*}$$

Vertex 50: $N[1720]^-({p_1})~-\Delta[1750][+1]({p_2})~-\gamma^{0}_{\nu }~( {p_3})~$

$$\begin{eqnarray*} &V_{50}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{365}-\... ...nu }f_{364}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{364}i) \end{eqnarray*}$$

Vertex 51: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[1750][+1]}({p_2})~- \Delta[1232][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{51}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{329}-\... ...nu }f_{328}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{328}i) \end{eqnarray*}$$

Vertex 52: $\Delta[1232][+1]^-({p_1})~-\Delta[1750][+1]({p_2})~-\gamma^{0}_{ \nu }~({p_3})~$

$$\begin{eqnarray*} &V_{52}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{329}-\... ...nu }f_{328}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{328}i) \end{eqnarray*}$$

Vertex 53: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[1750][+1]}({p_2})~- \Delta[1600][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{53}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{311}-\... ...nu }f_{310}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{310}i) \end{eqnarray*}$$

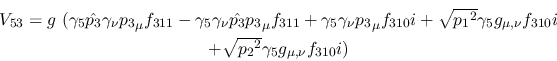
Vertex 54: $\Delta[1600][+1]^-({p_1})~-\Delta[1750][+1]({p_2})~-\gamma^{0}_{ \nu }~({p_3})~$

$$\begin{eqnarray*} &V_{54}=g~(\gamma_5{\hat {p_3}}\gamma_\nu {p_3}_\mu f_{311}-\... ...nu }f_{310}i \\ &+ \sqrt{{p_2}^2}\gamma_5g_{\mu , \nu }f_{310}i) \end{eqnarray*}$$

Vertex 55: $\gamma^{0}_{\nu }~({p_3})~-\overline{\Delta[1750][+1]}({p_2})~- \Delta[1700][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{55}=g~(- \sqrt{{p_1}^2}g_{\mu ,\nu }f_{293}i+ \sqrt{{p_2}... ...nu {\hat {p_3}}{p_3}_ \mu f_{292}+\gamma_\nu {p_3}_\mu f_{293}i) \end{eqnarray*}$$

Vertex 56: $\Delta[1700][+1]^-({p_1})~-\Delta[1750][+1]({p_2})~-\gamma^{0}_{ \nu }~({p_3})~$

$$\begin{eqnarray*} &V_{56}=g~( \sqrt{{p_1}^2}g_{\mu ,\nu }f_{293}i- \sqrt{{p_2}^... ...nu {\hat {p_3}}{p_3}_ \mu f_{292}+\gamma_\nu {p_3}_\mu f_{293}i) \end{eqnarray*}$$

Vertex 57: $\gamma^{0}_{\mu }~({p_3})~-\overline{P}({p_2})~-\Delta[1750][+1]( {p_1})~$

$$\begin{eqnarray*} &V_{57}=f_{128}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 58: $\overline{\Delta[1750][+1]}({p_1})~-P({p_2})~-\gamma^{0}_{\mu }~( {p_3})~$

$$\begin{eqnarray*} &V_{58}=f_{128}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 59: $\gamma^{0}_{\mu }~({p_3})~-\overline{N[1440]}({p_2})~- \Delta[1750][+1]({p_1})~$

$$\begin{eqnarray*} &V_{59}=f_{127}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 60: $\overline{\Delta[1750][+1]}({p_1})~-N[1440]({p_2})~-\gamma^{0}_{ \mu }~({p_3})~$

$$\begin{eqnarray*} &V_{60}=f_{127}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 61: $\gamma^{0}_{\mu }~({p_3})~-\overline{N[1535]}({p_2})~- \Delta[1750][+1]({p_1})~$

$$\begin{eqnarray*} &V_{61}=f_{126}g~(-\gamma_5{\hat {p_3}}\gamma_\mu +\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 62: $\overline{\Delta[1750][+1]}({p_1})~-N[1535]({p_2})~-\gamma^{0}_{ \mu }~({p_3})~$

$$\begin{eqnarray*} &V_{62}=f_{126}g~(\gamma_5{\hat {p_3}}\gamma_\mu -\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 63: $\gamma^{0}_{\mu }~({p_3})~-\overline{N[1650]}({p_2})~- \Delta[1750][+1]({p_1})~$

$$\begin{eqnarray*} &V_{63}=f_{125}g~(-\gamma_5{\hat {p_3}}\gamma_\mu +\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 64: $\overline{\Delta[1750][+1]}({p_1})~-N[1650]({p_2})~-\gamma^{0}_{ \mu }~({p_3})~$

$$\begin{eqnarray*} &V_{64}=f_{125}g~(\gamma_5{\hat {p_3}}\gamma_\mu -\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 65: $\gamma^{0}_{\mu }~({p_3})~-\overline{N[1710]}({p_2})~- \Delta[1750][+1]({p_1})~$

$$\begin{eqnarray*} &V_{65}=f_{124}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 66: $\overline{\Delta[1750][+1]}({p_1})~-N[1710]({p_2})~-\gamma^{0}_{ \mu }~({p_3})~$

$$\begin{eqnarray*} &V_{66}=f_{124}g~({\hat {p_3}}\gamma_\mu -\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 67: $\gamma^{0}_{\mu }~({p_3})~-\overline{\Delta[1620][+1]}({p_2})~- \Delta[1750][+1]({p_1})~$

$$\begin{eqnarray*} &V_{67}=f_{123}g~(-\gamma_5{\hat {p_3}}\gamma_\mu +\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 68: $\overline{\Delta[1750][+1]}({p_1})~-\Delta[1620][+1]({p_2})~- \gamma^{0}_{\mu }~({p_3})~$

$$\begin{eqnarray*} &V_{68}=f_{123}g~(\gamma_5{\hat {p_3}}\gamma_\mu -\gamma_5\gamma_\mu {\hat {p_3}}) \end{eqnarray*}$$

Vertex 69: $\pi^0({p_3})~-\overline{\Delta[1750][+1]}({p_2})~-N[1520]^+({p_1} )~$

$$\begin{eqnarray*} &V_{69}=-f_{103}gi~\gamma_5{p_2}_\mu \end{eqnarray*}$$

Vertex 70: $N[1520]^-({p_1})~-\Delta[1750][+1]({p_2})~-\pi^0({p_3})~$

$$\begin{eqnarray*} &V_{70}=f_{103}gi~\gamma_5{p_2}_\mu \end{eqnarray*}$$

Vertex 71: $\pi^0({p_3})~-\overline{\Delta[1750][+1]}({p_2})~- \Delta[1232][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{71}=-f_{68}g~{p_2}_\mu \end{eqnarray*}$$

Vertex 72: $\Delta[1232][+1]^-({p_1})~-\Delta[1750][+1]({p_2})~-\pi^0({p_3})~$

$$\begin{eqnarray*} &V_{72}=f_{68}g~{p_2}_\mu \end{eqnarray*}$$

Vertex 73: $\pi^0({p_3})~-\overline{\Delta[1750][+1]}({p_2})~- \Delta[1600][+1]^+({p_1})~$

$$\begin{eqnarray*} &V_{73}=-f_{62}g~{p_2}_\mu \end{eqnarray*}$$

Vertex 74: $\Delta[1600][+1]^-({p_1})~-\Delta[1750][+1]({p_2})~-\pi^0({p_3})~$

$$\begin{eqnarray*} &V_{74}=f_{62}g~{p_2}_\mu \end{eqnarray*}$$

Vertex 75: $\pi^0({p_3})~-\overline{P}({p_2})~-\Delta[1750][+1]({p_1})~$

$$\begin{eqnarray*} &V_{75}=-f_{20}g~\gamma_5 \end{eqnarray*}$$

Vertex 76: $\overline{\Delta[1750][+1]}({p_1})~-P({p_2})~-\pi^0({p_3})~$

$$\begin{eqnarray*} &V_{76}=f_{20}g~\gamma_5 \end{eqnarray*}$$

Vertex 77: $\pi^0({p_3})~-\overline{N[1440]}({p_2})~-\Delta[1750][+1]({p_1})~$

$$\begin{eqnarray*} &V_{77}=-f_{18}g~\gamma_5 \end{eqnarray*}$$

Vertex 78: $\overline{\Delta[1750][+1]}({p_1})~-N[1440]({p_2})~-\pi^0({p_3})~$

$$\begin{eqnarray*} &V_{78}=f_{18}g~\gamma_5 \end{eqnarray*}$$

Vertex 79: $\pi^0({p_3})~-\overline{N[1535]}({p_2})~-\Delta[1750][+1]({p_1})~$

$$\begin{eqnarray*} &V_{79}=-f_{17}gi \end{eqnarray*}$$

Vertex 80: $\overline{\Delta[1750][+1]}({p_1})~-N[1535]({p_2})~-\pi^0({p_3})~$

$$\begin{eqnarray*} &V_{80}=f_{17}gi \end{eqnarray*}$$