squark-squark-squark-squark 134 Vertices

There are 134 vertices in the section

Vertex 823 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{t_{1}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{t_{1}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(823)=\displaystyle{cos^{2}{\theta_t}~sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(823)=0\end{eqnarray*}$$

Vertex 824 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{t_{1}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{t_{2}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(824)=\displaystyle{{\sin (2{\theta_t})} ~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(824)=0 \end{eqnarray*}$$

Vertex 825 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{t_{2}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{t_{1}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(825)=\displaystyle{{\sin (2{\theta_t})} ~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(825)=0 \end{eqnarray*}$$

Vertex 826 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{t_{2}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{t_{2}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(826)=\displaystyle{sin^{2}{\theta_w}~sin^{2}{\theta_t}~g^2~i~ \over 9}&{a_2^ {SSSS}}(826)=0\end{eqnarray*}$$

Vertex 827 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{t_{1}}}_{{i_1}}~({p_1})~- \tilde{u_{L}}_{{i_4}}~({p_4})~-\tilde{t_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(827)=\displaystyle{g^2~i~ \over 36}(-4~cos^{2}{... ...-5~cos^{2}{\theta_t}~+4~sin^{2} {\theta_w}~)&{a_2^ {SSSS}}(827)=0\end{eqnarray*}$$

Vertex 828 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{t_{1}}}_{{i_1}}~({p_1})~- \tilde{u_{L}}_{{i_4}}~({p_4})~-\tilde{t_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(828)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~ \over 72}(-2~{\cos (2{\theta_w})} ~-7)&{a_2^ {SSSS}}(828)=0 \end{eqnarray*}$$

Vertex 829 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{t_{2}}}_{{i_1}}~({p_1})~- \tilde{u_{L}}_{{i_4}}~({p_4})~-\tilde{t_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(829)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~ \over 72}(-2~{\cos (2{\theta_w})} ~-7)&{a_2^ {SSSS}}(829)=0 \end{eqnarray*}$$

Vertex 830 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{t_{2}}}_{{i_1}}~({p_1})~- \tilde{u_{L}}_{{i_4}}~({p_4})~-\tilde{t_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(830)=\displaystyle{g^2~i~ \over 36}(-4~cos^{2}{... ...+4~sin^{2}{\theta_w}~-5~sin^{2} {\theta_t}~)&{a_2^ {SSSS}}(830)=0\end{eqnarray*}$$

Vertex 831 and type=12: $\overline{\tilde{s_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{s_{R}}_{{i_3}}~({p_2})~-\tilde{t_{1}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(831)=\displaystyle{-cos^{2}{\theta_t}~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(831)=0 \end{eqnarray*}$$

Vertex 832 and type=12: $\overline{\tilde{s_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{s_{R}}_{{i_3}}~({p_2})~-\tilde{t_{2}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(832)=\displaystyle{-{\sin (2{\theta_t})} ~sin^{2}{\theta_w}~g^2~i~ \over 36}&{a_2^ {SSSS}}(832)=0 \end{eqnarray*}$$

Vertex 833 and type=12: $\overline{\tilde{s_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{s_{R}}_{{i_3}}~({p_2})~-\tilde{t_{1}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(833)=\displaystyle{-{\sin (2{\theta_t})} ~sin^{2}{\theta_w}~g^2~i~ \over 36}&{a_2^ {SSSS}}(833)=0 \end{eqnarray*}$$

Vertex 834 and type=12: $\overline{\tilde{s_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{s_{R}}_{{i_3}}~({p_2})~-\tilde{t_{2}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(834)=\displaystyle{-sin^{2}{\theta_w}~sin^{2}{\theta_t}~g^2~i~ \over 18}&{a_2^ {SSSS}}(834)=0 \end{eqnarray*}$$

Vertex 835 and type=12: $\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{s_{L}}_{{i_4}}~({p_2})~-\tilde{t_{1}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(835)=\displaystyle{g^2~i~ \over 72}(7~{\cos (2{... ...2{\theta_w})} ~ +2~{\cos (2{\theta_t})} ~+6)&{a_2^ {SSSS}}(835)=0\end{eqnarray*}$$

Vertex 836 and type=12: $\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{s_{L}}_{{i_4}}~({p_2})~-\tilde{t_{2}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(836)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~ \over 72}(7~{\cos (2{\theta_w})} ~+2)&{a_2^ {SSSS}}(836)=0 \end{eqnarray*}$$

Vertex 837 and type=12: $\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{s_{L}}_{{i_4}}~({p_2})~-\tilde{t_{1}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(837)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~ \over 72}(7~{\cos (2{\theta_w})} ~+2)&{a_2^ {SSSS}}(837)=0 \end{eqnarray*}$$

Vertex 838 and type=12: $\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{s_{L}}_{{i_4}}~({p_2})~-\tilde{t_{2}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(838)=\displaystyle{g^2~i~ \over 72}(-7~{\cos (2... ...2{\theta_w})} ~-2~{\cos (2{\theta_t})} ~+6)&{a_2^ {SSSS}}(838)=0\end{eqnarray*}$$

Vertex 839 and type=12: $\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_4}}~({p_2})~-\tilde{b_{1}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(839)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_b}} ~{\cos {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 839)=0\end{eqnarray*}$$

Vertex 840 and type=12: $\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_4}}~({p_2})~-\tilde{b_{2}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(840)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_t}} ~{\sin {\theta_b}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 840)=0\end{eqnarray*}$$

Vertex 841 and type=12: $\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_4}}~({p_2})~-\tilde{b_{1}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(841)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_b}} ~{\sin {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 841)=0\end{eqnarray*}$$

Vertex 842 and type=12: $\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_4}}~({p_2})~-\tilde{b_{2}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(842)=\displaystyle{-cos^{2}{\theta_w}~{\sin {\theta_b}} ~{\sin {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 842)=0\end{eqnarray*}$$

Vertex 843 and type=12: $\overline{\tilde{d_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{d_{R}}_{{i_3}}~({p_2})~-\tilde{t_{1}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(843)=\displaystyle{-cos^{2}{\theta_t}~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(843)=0 \end{eqnarray*}$$

Vertex 844 and type=12: $\overline{\tilde{d_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{d_{R}}_{{i_3}}~({p_2})~-\tilde{t_{2}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(844)=\displaystyle{-{\sin (2{\theta_t})} ~sin^{2}{\theta_w}~g^2~i~ \over 36}&{a_2^ {SSSS}}(844)=0 \end{eqnarray*}$$

Vertex 845 and type=12: $\overline{\tilde{d_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{d_{R}}_{{i_3}}~({p_2})~-\tilde{t_{1}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(845)=\displaystyle{-{\sin (2{\theta_t})} ~sin^{2}{\theta_w}~g^2~i~ \over 36}&{a_2^ {SSSS}}(845)=0 \end{eqnarray*}$$

Vertex 846 and type=12: $\overline{\tilde{d_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{d_{R}}_{{i_3}}~({p_2})~-\tilde{t_{2}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(846)=\displaystyle{-sin^{2}{\theta_w}~sin^{2}{\theta_t}~g^2~i~ \over 18}&{a_2^ {SSSS}}(846)=0 \end{eqnarray*}$$

Vertex 847 and type=12: $\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{u_{L}}_{{i_4}}~({p_2})~-\tilde{b_{1}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(847)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_b}} ~{\cos {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 847)=0\end{eqnarray*}$$

Vertex 848 and type=12: $\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{u_{L}}_{{i_4}}~({p_2})~-\tilde{b_{2}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(848)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_t}} ~{\sin {\theta_b}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 848)=0\end{eqnarray*}$$

Vertex 849 and type=12: $\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{u_{L}}_{{i_4}}~({p_2})~-\tilde{b_{1}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(849)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_b}} ~{\sin {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 849)=0\end{eqnarray*}$$

Vertex 850 and type=12: $\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{u_{L}}_{{i_4}}~({p_2})~-\tilde{b_{2}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(850)=\displaystyle{-cos^{2}{\theta_w}~{\sin {\theta_b}} ~{\sin {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 850)=0\end{eqnarray*}$$

Vertex 851 and type=12: $\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{d_{L}}_{{i_4}}~({p_2})~-\tilde{t_{1}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(851)=\displaystyle{g^2~i~ \over 72}(7~{\cos (2{... ...2{\theta_w})} ~ +2~{\cos (2{\theta_t})} ~+6)&{a_2^ {SSSS}}(851)=0\end{eqnarray*}$$

Vertex 852 and type=12: $\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{d_{L}}_{{i_4}}~({p_2})~-\tilde{t_{2}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(852)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~ \over 72}(7~{\cos (2{\theta_w})} ~+2)&{a_2^ {SSSS}}(852)=0 \end{eqnarray*}$$

Vertex 853 and type=12: $\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{d_{L}}_{{i_4}}~({p_2})~-\tilde{t_{1}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(853)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~ \over 72}(7~{\cos (2{\theta_w})} ~+2)&{a_2^ {SSSS}}(853)=0 \end{eqnarray*}$$

Vertex 854 and type=12: $\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{d_{L}}_{{i_4}}~({p_2})~-\tilde{t_{2}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(854)=\displaystyle{g^2~i~ \over 72}(-7~{\cos (2... ...2{\theta_w})} ~-2~{\cos (2{\theta_t})} ~+6)&{a_2^ {SSSS}}(854)=0\end{eqnarray*}$$

Vertex 855 and type=12: $\overline{\tilde{c_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{c_{R}}_{{i_3}}~({p_2})~-\tilde{t_{1}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(855)=\displaystyle{cos^{2}{\theta_t}~sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(855)=0\end{eqnarray*}$$

Vertex 856 and type=12: $\overline{\tilde{c_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{c_{R}}_{{i_3}}~({p_2})~-\tilde{t_{2}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(856)=\displaystyle{{\sin (2{\theta_t})} ~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(856)=0 \end{eqnarray*}$$

Vertex 857 and type=12: $\overline{\tilde{c_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{c_{R}}_{{i_3}}~({p_2})~-\tilde{t_{1}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(857)=\displaystyle{{\sin (2{\theta_t})} ~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(857)=0 \end{eqnarray*}$$

Vertex 858 and type=12: $\overline{\tilde{c_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{c_{R}}_{{i_3}}~({p_2})~-\tilde{t_{2}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(858)=\displaystyle{sin^{2}{\theta_w}~sin^{2}{\theta_t}~g^2~i~ \over 9}&{a_2^ {SSSS}}(858)=0\end{eqnarray*}$$

Vertex 859 and type=12: $\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_4}}~({p_2})~-\tilde{t_{1}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(859)=\displaystyle{g^2~i~ \over 36}(-4~cos^{2}{... ...-5~cos^{2}{\theta_t}~+4~sin^{2} {\theta_w}~)&{a_2^ {SSSS}}(859)=0\end{eqnarray*}$$

Vertex 860 and type=12: $\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_4}}~({p_2})~-\tilde{t_{2}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(860)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~ \over 72}(-2~{\cos (2{\theta_w})} ~-7)&{a_2^ {SSSS}}(860)=0 \end{eqnarray*}$$

Vertex 861 and type=12: $\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_4}}~({p_2})~-\tilde{t_{1}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(861)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~ \over 72}(-2~{\cos (2{\theta_w})} ~-7)&{a_2^ {SSSS}}(861)=0 \end{eqnarray*}$$

Vertex 862 and type=12: $\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_4}}~({p_2})~-\tilde{t_{2}}_{{i_3}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(862)=\displaystyle{g^2~i~ \over 36}(-4~cos^{2}{... ...+4~sin^{2}{\theta_w}~-5~sin^{2} {\theta_t}~)&{a_2^ {SSSS}}(862)=0\end{eqnarray*}$$

Vertex 863 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{d_{L}}_{{i_4}}~({p_4})~-\tilde{t_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(863)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_b}} ~{\cos {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 863)=0\end{eqnarray*}$$

Vertex 864 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{d_{L}}_{{i_4}}~({p_4})~-\tilde{t_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(864)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_b}} ~{\sin {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 864)=0\end{eqnarray*}$$

Vertex 865 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{d_{L}}_{{i_4}}~({p_4})~-\tilde{t_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(865)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_t}} ~{\sin {\theta_b}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 865)=0\end{eqnarray*}$$

Vertex 866 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{d_{L}}_{{i_4}}~({p_4})~-\tilde{t_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(866)=\displaystyle{-cos^{2}{\theta_w}~{\sin {\theta_b}} ~{\sin {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 866)=0\end{eqnarray*}$$

Vertex 867 and type=12: $\overline{\tilde{c_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{s_{L}}_{{i_4}}~({p_4})~-\tilde{t_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(867)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_b}} ~{\cos {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 867)=0\end{eqnarray*}$$

Vertex 868 and type=12: $\overline{\tilde{c_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{s_{L}}_{{i_4}}~({p_4})~-\tilde{t_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(868)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_b}} ~{\sin {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 868)=0\end{eqnarray*}$$

Vertex 869 and type=12: $\overline{\tilde{c_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{s_{L}}_{{i_4}}~({p_4})~-\tilde{t_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(869)=\displaystyle{-cos^{2}{\theta_w}~{\cos {\theta_t}} ~{\sin {\theta_b}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 869)=0\end{eqnarray*}$$

Vertex 870 and type=12: $\overline{\tilde{c_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{s_{L}}_{{i_4}}~({p_4})~-\tilde{t_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(870)=\displaystyle{-cos^{2}{\theta_w}~{\sin {\theta_b}} ~{\sin {\theta_t}} ~g^2~i~ \over 2}&{a_2^ {SSSS}}( 870)=0\end{eqnarray*}$$

Vertex 871 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{b_{1}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(871)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 18}(-{\cos (2{\theta_b})} +3)&{a_2^ {SSSS}}(871)=0 \end{eqnarray*}$$

Vertex 872 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{b_{2}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(872)=\displaystyle{-{\sin (2{\theta_b})} ~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(872)=0 \end{eqnarray*}$$

Vertex 873 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{b_{1}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(873)=\displaystyle{-{\sin (2{\theta_b})} ~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(873)=0 \end{eqnarray*}$$

Vertex 874 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{b_{2}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(874)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 18}({\cos (2{\theta_b})} +3)&{a_2^ {SSSS}}(874)=0 \end{eqnarray*}$$

Vertex 875 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{u_{L}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(875)=\displaystyle{g^2~i~ \over 72}(4~{\cos (2{... ...2{\theta_w})} ~ +5~{\cos (2{\theta_b})} ~+3)&{a_2^ {SSSS}}(875)=0\end{eqnarray*}$$

Vertex 876 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{u_{L}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(876)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~ \over 72}(4~{\cos (2{\theta_w})} ~+5)&{a_2^ {SSSS}}(876)=0 \end{eqnarray*}$$

Vertex 877 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{u_{L}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(877)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~ \over 72}(4~{\cos (2{\theta_w})} ~+5)&{a_2^ {SSSS}}(877)=0 \end{eqnarray*}$$

Vertex 878 and type=12: $\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{u_{L}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(878)=\displaystyle{g^2~i~ \over 72}(-4~{\cos (2... ...2{\theta_w})} ~-5~{\cos (2{\theta_b})} ~+3)&{a_2^ {SSSS}}(878)=0\end{eqnarray*}$$

Vertex 879 and type=12: $\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{t_{1}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(879)=\displaystyle{g^2~i~ \over 72~sin^{2}{\bet... ...{m_{Z}}^2~ \\ &-9~cos^{2}{\theta_t}~sin^{2}{\theta_b}~{m_{b}}^2~)\end{eqnarray*}$$

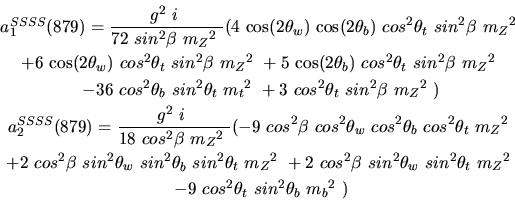
Vertex 880 and type=12: $\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{t_{1}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(880)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~... ..._w}~sin^{2}{\theta_t}~ {m_{Z}}^2~+9~cos^{2}{\theta_t}~{m_{b}}^2~)\end{eqnarray*}$$

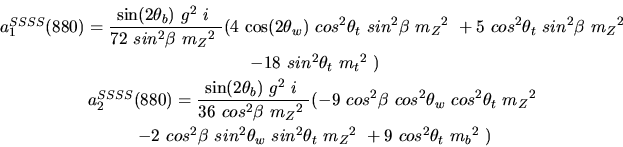
Vertex 881 and type=12: $\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{t_{1}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(881)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~... ...a_w}~sin^{2}{\theta_b}~{m_{Z}}^2~-9~sin^{2}{\theta_b}~{m_{b}}^2~)\end{eqnarray*}$$

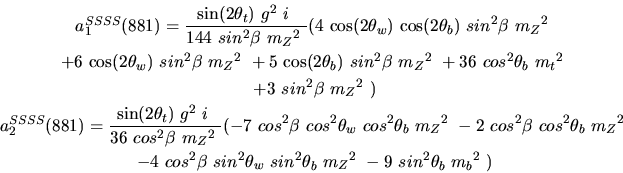
Vertex 882 and type=12: $\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{t_{1}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(882)=\displaystyle{{\sin (2{\theta_b})} ~{\sin ... ...^{2}{\beta}~{m_{Z}}^2~-7~cos^{2}{\beta}~{m_{Z}}^2~+18~{m_{b}}^2~)\end{eqnarray*}$$

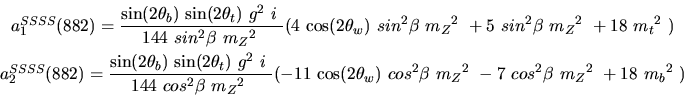
Vertex 883 and type=12: $\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{t_{1}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(883)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~... ..._w}~sin^{2}{\theta_t}~ {m_{Z}}^2~+9~cos^{2}{\theta_t}~{m_{b}}^2~)\end{eqnarray*}$$

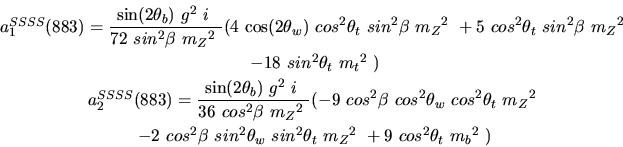
Vertex 884 and type=12: $\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{t_{1}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(884)=\displaystyle{g^2~i~ \over 72~sin^{2}{\bet... ...{m_{Z}}^2~ \\ &-9~cos^{2}{\theta_b}~cos^{2}{\theta_t}~{m_{b}}^2~)\end{eqnarray*}$$

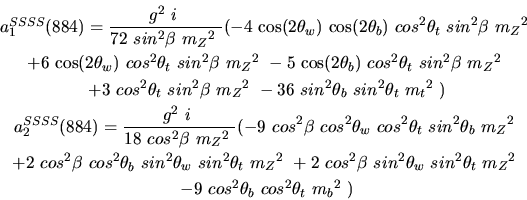
Vertex 885 and type=12: $\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{t_{1}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(885)=\displaystyle{{\sin (2{\theta_b})} ~{\sin ... ...^{2}{\beta}~{m_{Z}}^2~-7~cos^{2}{\beta}~{m_{Z}}^2~+18~{m_{b}}^2~)\end{eqnarray*}$$

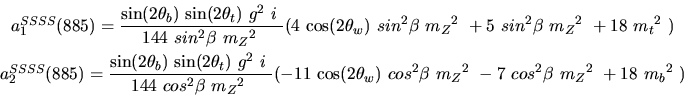
Vertex 886 and type=12: $\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{t_{1}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(886)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~... ...eta}~sin^{2}{\theta_w}~{m_{Z}}^2~-9~cos^{2}{\theta_b}~{m_{b}}^2~)\end{eqnarray*}$$

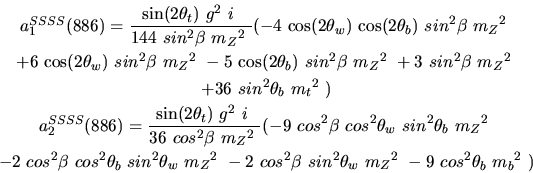
Vertex 887 and type=12: $\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{t_{2}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(887)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~... ...a_w}~sin^{2}{\theta_b}~{m_{Z}}^2~-9~sin^{2}{\theta_b}~{m_{b}}^2~)\end{eqnarray*}$$

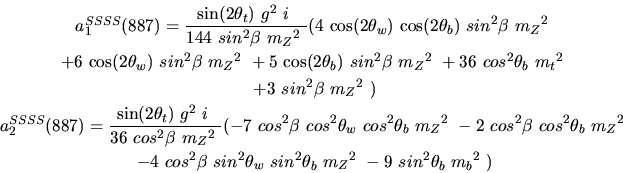
Vertex 888 and type=12: $\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{t_{2}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(888)=\displaystyle{{\sin (2{\theta_b})} ~{\sin ... ...^{2}{\beta}~{m_{Z}}^2~-7~cos^{2}{\beta}~{m_{Z}}^2~+18~{m_{b}}^2~)\end{eqnarray*}$$

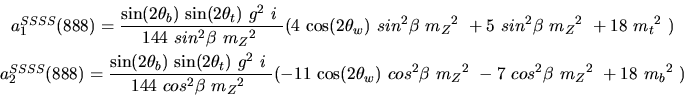
Vertex 889 and type=12: $\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{t_{2}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(889)=\displaystyle{g^2~i~ \over 72~sin^{2}{\bet... ...{m_{Z}}^2~ \\ &-9~sin^{2}{\theta_b}~sin^{2}{\theta_t}~{m_{b}}^2~)\end{eqnarray*}$$

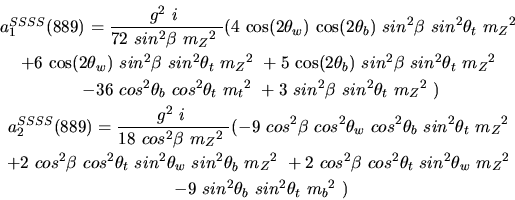
Vertex 890 and type=12: $\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{t_{2}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(890)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~... ..._t}~sin^{2}{\theta_w}~ {m_{Z}}^2~+9~sin^{2}{\theta_t}~{m_{b}}^2~)\end{eqnarray*}$$

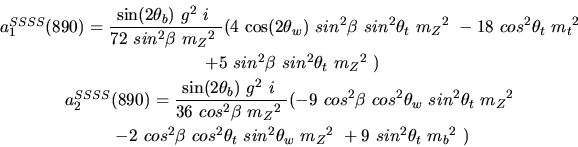
Vertex 891 and type=12: $\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{t_{2}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(891)=\displaystyle{{\sin (2{\theta_b})} ~{\sin ... ...^{2}{\beta}~{m_{Z}}^2~-7~cos^{2}{\beta}~{m_{Z}}^2~+18~{m_{b}}^2~)\end{eqnarray*}$$

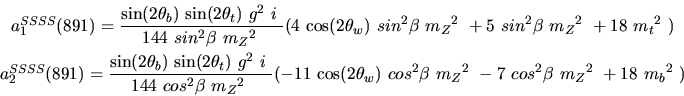
Vertex 892 and type=12: $\overline{\tilde{t_{1}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{t_{2}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(892)=\displaystyle{{\sin (2{\theta_t})} ~g^2~i~... ...eta}~sin^{2}{\theta_w}~{m_{Z}}^2~-9~cos^{2}{\theta_b}~{m_{b}}^2~)\end{eqnarray*}$$

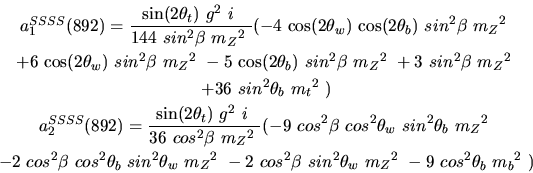
Vertex 893 and type=12: $\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{t_{2}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(893)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~... ..._t}~sin^{2}{\theta_w}~ {m_{Z}}^2~+9~sin^{2}{\theta_t}~{m_{b}}^2~)\end{eqnarray*}$$

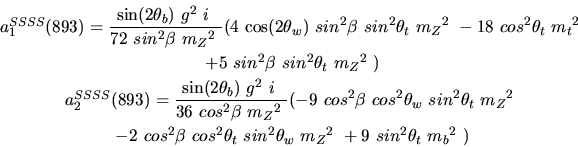
Vertex 894 and type=12: $\overline{\tilde{t_{2}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{t_{2}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(894)=\displaystyle{g^2~i~ \over 72~sin^{2}{\bet... ...{m_{Z}}^2~ \\ &-9~cos^{2}{\theta_b}~sin^{2}{\theta_t}~{m_{b}}^2~)\end{eqnarray*}$$

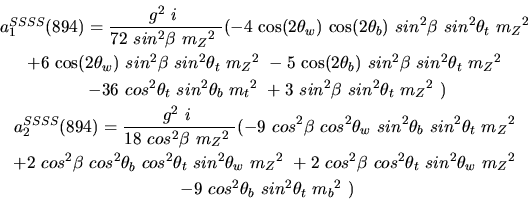
Vertex 895 and type=12: $\overline{\tilde{s_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{s_{R}}_{{i_3}}~({p_4})~-\tilde{b_{1}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(895)=\displaystyle{-cos^{2}{\theta_b}~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(895)=0 \end{eqnarray*}$$

Vertex 896 and type=12: $\overline{\tilde{s_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{s_{R}}_{{i_3}}~({p_4})~-\tilde{b_{2}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(896)=\displaystyle{-{\sin (2{\theta_b})} ~sin^{2}{\theta_w}~g^2~i~ \over 36}&{a_2^ {SSSS}}(896)=0 \end{eqnarray*}$$

Vertex 897 and type=12: $\overline{\tilde{s_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{s_{R}}_{{i_3}}~({p_4})~-\tilde{b_{1}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(897)=\displaystyle{-{\sin (2{\theta_b})} ~sin^{2}{\theta_w}~g^2~i~ \over 36}&{a_2^ {SSSS}}(897)=0 \end{eqnarray*}$$

Vertex 898 and type=12: $\overline{\tilde{s_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{s_{R}}_{{i_3}}~({p_4})~-\tilde{b_{2}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(898)=\displaystyle{-sin^{2}{\theta_w}~sin^{2}{\theta_b}~g^2~i~ \over 18}&{a_2^ {SSSS}}(898)=0 \end{eqnarray*}$$

Vertex 899 and type=12: $\overline{\tilde{s_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{s_{L}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(899)=\displaystyle{g^2~i~ \over 72}(-5~{\cos (2... ...2{\theta_w})} ~-4~{\cos (2{\theta_b})} ~-6)&{a_2^ {SSSS}}(899)=0\end{eqnarray*}$$

Vertex 900 and type=12: $\overline{\tilde{s_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{s_{L}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(900)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~ \over 72}(-5~{\cos (2{\theta_w})} ~-4)&{a_2^ {SSSS}}(900)=0 \end{eqnarray*}$$

Vertex 901 and type=12: $\overline{\tilde{s_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{s_{L}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(901)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~ \over 72}(-5~{\cos (2{\theta_w})} ~-4)&{a_2^ {SSSS}}(901)=0 \end{eqnarray*}$$

Vertex 902 and type=12: $\overline{\tilde{s_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{s_{L}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(902)=\displaystyle{g^2~i~ \over 72}(5~{\cos (2{... ...2{\theta_w})} ~ +4~{\cos (2{\theta_b})} ~-6)&{a_2^ {SSSS}}(902)=0\end{eqnarray*}$$

Vertex 903 and type=12: $\overline{\tilde{d_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{d_{R}}_{{i_3}}~({p_4})~-\tilde{b_{1}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(903)=\displaystyle{-cos^{2}{\theta_b}~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(903)=0 \end{eqnarray*}$$

Vertex 904 and type=12: $\overline{\tilde{d_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{d_{R}}_{{i_3}}~({p_4})~-\tilde{b_{2}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(904)=\displaystyle{-{\sin (2{\theta_b})} ~sin^{2}{\theta_w}~g^2~i~ \over 36}&{a_2^ {SSSS}}(904)=0 \end{eqnarray*}$$

Vertex 905 and type=12: $\overline{\tilde{d_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{d_{R}}_{{i_3}}~({p_4})~-\tilde{b_{1}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(905)=\displaystyle{-{\sin (2{\theta_b})} ~sin^{2}{\theta_w}~g^2~i~ \over 36}&{a_2^ {SSSS}}(905)=0 \end{eqnarray*}$$

Vertex 906 and type=12: $\overline{\tilde{d_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{d_{R}}_{{i_3}}~({p_4})~-\tilde{b_{2}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(906)=\displaystyle{-sin^{2}{\theta_w}~sin^{2}{\theta_b}~g^2~i~ \over 18}&{a_2^ {SSSS}}(906)=0 \end{eqnarray*}$$

Vertex 907 and type=12: $\overline{\tilde{d_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{d_{L}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(907)=\displaystyle{g^2~i~ \over 72}(-5~{\cos (2... ...2{\theta_w})} ~-4~{\cos (2{\theta_b})} ~-6)&{a_2^ {SSSS}}(907)=0\end{eqnarray*}$$

Vertex 908 and type=12: $\overline{\tilde{d_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{d_{L}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(908)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~ \over 72}(-5~{\cos (2{\theta_w})} ~-4)&{a_2^ {SSSS}}(908)=0 \end{eqnarray*}$$

Vertex 909 and type=12: $\overline{\tilde{d_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{d_{L}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(909)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~ \over 72}(-5~{\cos (2{\theta_w})} ~-4)&{a_2^ {SSSS}}(909)=0 \end{eqnarray*}$$

Vertex 910 and type=12: $\overline{\tilde{d_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{d_{L}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(910)=\displaystyle{g^2~i~ \over 72}(5~{\cos (2{... ...2{\theta_w})} ~ +4~{\cos (2{\theta_b})} ~-6)&{a_2^ {SSSS}}(910)=0\end{eqnarray*}$$

Vertex 911 and type=12: $\overline{\tilde{c_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{c_{R}}_{{i_3}}~({p_4})~-\tilde{b_{1}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(911)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 18}(-{\cos (2{\theta_b})} +3)&{a_2^ {SSSS}}(911)=0 \end{eqnarray*}$$

Vertex 912 and type=12: $\overline{\tilde{c_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{c_{R}}_{{i_3}}~({p_4})~-\tilde{b_{2}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(912)=\displaystyle{-{\sin (2{\theta_b})} ~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(912)=0 \end{eqnarray*}$$

Vertex 913 and type=12: $\overline{\tilde{c_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{c_{R}}_{{i_3}}~({p_4})~-\tilde{b_{1}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(913)=\displaystyle{-{\sin (2{\theta_b})} ~sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(913)=0 \end{eqnarray*}$$

Vertex 914 and type=12: $\overline{\tilde{c_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{c_{R}}_{{i_3}}~({p_4})~-\tilde{b_{2}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(914)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 18}({\cos (2{\theta_b})} +3)&{a_2^ {SSSS}}(914)=0 \end{eqnarray*}$$

Vertex 915 and type=12: $\overline{\tilde{c_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{c_{L}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(915)=\displaystyle{g^2~i~ \over 72}(4~{\cos (2{... ...2{\theta_w})} ~ +5~{\cos (2{\theta_b})} ~+3)&{a_2^ {SSSS}}(915)=0\end{eqnarray*}$$

Vertex 916 and type=12: $\overline{\tilde{c_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{1}}}_{{i_1}}~({p_1})~- \tilde{c_{L}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(916)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~ \over 72}(4~{\cos (2{\theta_w})} ~+5)&{a_2^ {SSSS}}(916)=0 \end{eqnarray*}$$

Vertex 917 and type=12: $\overline{\tilde{c_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{c_{L}}_{{i_4}}~({p_4})~-\tilde{b_{1}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(917)=\displaystyle{{\sin (2{\theta_b})} ~g^2~i~ \over 72}(4~{\cos (2{\theta_w})} ~+5)&{a_2^ {SSSS}}(917)=0 \end{eqnarray*}$$

Vertex 918 and type=12: $\overline{\tilde{c_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{b_{2}}}_{{i_1}}~({p_1})~- \tilde{c_{L}}_{{i_4}}~({p_4})~-\tilde{b_{2}}_{{i_3}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(918)=\displaystyle{g^2~i~ \over 72}(-4~{\cos (2... ...2{\theta_w})} ~-5~{\cos (2{\theta_b})} ~+3)&{a_2^ {SSSS}}(918)=0\end{eqnarray*}$$

Vertex 919 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{u_{L}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{u_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(919)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(919)=0\end{eqnarray*}$$

Vertex 920 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{s_{R}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{s_{R}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(920)=\displaystyle{2~sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(920)=0\end{eqnarray*}$$

Vertex 921 and type=12: $\overline{\tilde{s_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~- \tilde{s_{R}}_{{i_3}}~({p_2})~-\tilde{u_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(921)=\displaystyle{-sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(921)=0\end{eqnarray*}$$

Vertex 922 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{s_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(922)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(922)=0\end{eqnarray*}$$

Vertex 923 and type=12: $\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~- \tilde{s_{L}}_{{i_3}}~({p_2})~-\tilde{u_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(923)=\displaystyle{g^2~i~ \over 36}(5~{\cos (2{\theta_w})} ~+4)&{a_2^ {SSSS}}(923)=0\end{eqnarray*}$$

Vertex 924 and type=12: $\overline{\tilde{s_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~- \tilde{s_{R}}_{{i_3}}~({p_4})~-\tilde{s_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(924)=\displaystyle{-sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(924)=0\end{eqnarray*}$$

Vertex 925 and type=12: $\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_3}}~({p_2})~-\tilde{d_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(925)=\displaystyle{-cos^{2}{\theta_w}~g^2~i~ \over 2}&{a_2^ {SSSS}}(925)=0\end{eqnarray*}$$

Vertex 926 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{d_{R}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{d_{R}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(926)=\displaystyle{2~sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(926)=0\end{eqnarray*}$$

Vertex 927 and type=12: $\overline{\tilde{d_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~- \tilde{d_{R}}_{{i_3}}~({p_2})~-\tilde{u_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(927)=\displaystyle{-sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(927)=0\end{eqnarray*}$$

Vertex 928 and type=12: $\overline{\tilde{s_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{d_{R}}}_{{i_1}}~({p_1})~- \tilde{s_{R}}_{{i_3}}~({p_4})~-\tilde{d_{R}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(928)=\displaystyle{-sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(928)=0\end{eqnarray*}$$

Vertex 929 and type=12: $\overline{\tilde{d_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{s_{L}}}_{{i_2}}~({p_3})~- \tilde{d_{R}}_{{i_3}}~({p_2})~-\tilde{s_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(929)=\displaystyle{-sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(929)=0\end{eqnarray*}$$

Vertex 930 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{d_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(930)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(930)=0\end{eqnarray*}$$

Vertex 931 and type=12: $\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~- \tilde{d_{L}}_{{i_3}}~({p_2})~-\tilde{u_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(931)=\displaystyle{g^2~i~ \over 36}(5~{\cos (2{... ...2^ {SSSS}}(931)=\displaystyle{-cos^{2} {\theta_w}~g^2~i~ \over 2}\end{eqnarray*}$$

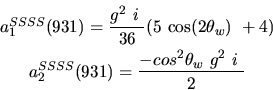
Vertex 932 and type=12: $\overline{\tilde{s_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~- \tilde{s_{R}}_{{i_3}}~({p_4})~-\tilde{d_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(932)=\displaystyle{-sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(932)=0\end{eqnarray*}$$

Vertex 933 and type=12: $\overline{\tilde{s_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~- \tilde{s_{L}}_{{i_3}}~({p_4})~-\tilde{d_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(933)=\displaystyle{g^2~i~ \over 36}(-4~{\cos (2{\theta_w})} ~-5)&{a_2^ {SSSS}}(933)=0\end{eqnarray*}$$

Vertex 934 and type=12: $\overline{\tilde{d_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~- \tilde{d_{R}}_{{i_3}}~({p_4})~-\tilde{d_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(934)=\displaystyle{-sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(934)=0\end{eqnarray*}$$

Vertex 935 and type=12: $\overline{\tilde{c_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~- \tilde{c_{R}}_{{i_3}}~({p_2})~-\tilde{u_{R}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(935)=\displaystyle{-4~sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(935)=0\end{eqnarray*}$$

Vertex 936 and type=12: $\overline{\tilde{c_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~- \tilde{c_{R}}_{{i_3}}~({p_2})~-\tilde{u_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(936)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(936)=0\end{eqnarray*}$$

Vertex 937 and type=12: $\overline{\tilde{c_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{s_{R}}}_{{i_2}}~({p_3})~- \tilde{c_{R}}_{{i_3}}~({p_2})~-\tilde{s_{R}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(937)=\displaystyle{2~sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(937)=0\end{eqnarray*}$$

Vertex 938 and type=12: $\overline{\tilde{c_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{s_{L}}}_{{i_2}}~({p_3})~- \tilde{c_{R}}_{{i_3}}~({p_2})~-\tilde{s_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(938)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(938)=0\end{eqnarray*}$$

Vertex 939 and type=12: $\overline{\tilde{c_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{d_{R}}}_{{i_2}}~({p_3})~- \tilde{c_{R}}_{{i_3}}~({p_2})~-\tilde{d_{R}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(939)=\displaystyle{2~sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(939)=0\end{eqnarray*}$$

Vertex 940 and type=12: $\overline{\tilde{c_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{d_{L}}}_{{i_2}}~({p_3})~- \tilde{c_{R}}_{{i_3}}~({p_2})~-\tilde{d_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(940)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(940)=0\end{eqnarray*}$$

Vertex 941 and type=12: $\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{d_{L}}}_{{i_2}}~({p_3})~- \tilde{s_{L}}_{{i_3}}~({p_2})~-\tilde{u_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(941)=\displaystyle{-cos^{2}{\theta_w}~g^2~i~ \over 2}&{a_2^ {SSSS}}(941)=0\end{eqnarray*}$$

Vertex 942 and type=12: $\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~- \tilde{u_{R}}_{{i_3}}~({p_4})~-\tilde{c_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(942)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(942)=0\end{eqnarray*}$$

Vertex 943 and type=12: $\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_3}}~({p_2})~-\tilde{u_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(943)=\displaystyle{g^2~i~ \over 36}(-4~{\cos (2{\theta_w})} ~-5)&{a_2^ {SSSS}}(943)=0\end{eqnarray*}$$

Vertex 944 and type=12: $\overline{\tilde{s_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~- \tilde{s_{R}}_{{i_3}}~({p_4})~-\tilde{c_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(944)=\displaystyle{-sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(944)=0\end{eqnarray*}$$

Vertex 945 and type=12: $\overline{\tilde{s_{L}}}_{{i_2}}~({p_3})~-\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~- \tilde{s_{L}}_{{i_3}}~({p_4})~-\tilde{c_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(945)=\displaystyle{g^2~i~ \over 36}(5~{\cos (2{... ...2^ {SSSS}}(945)=\displaystyle{-cos^{2} {\theta_w}~g^2~i~ \over 2}\end{eqnarray*}$$

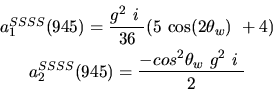
Vertex 946 and type=12: $\overline{\tilde{d_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~- \tilde{d_{R}}_{{i_3}}~({p_4})~-\tilde{c_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(946)=\displaystyle{-sin^{2}{\theta_w}~g^2~i~ \over 18}&{a_2^ {SSSS}}(946)=0\end{eqnarray*}$$

Vertex 947 and type=12: $\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{d_{L}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_3}}~({p_2})~-\tilde{d_{L}}_{{i_4}}~({p_4})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(947)=\displaystyle{g^2~i~ \over 36}(5~{\cos (2{\theta_w})} ~+4)&{a_2^ {SSSS}}(947)=0\end{eqnarray*}$$

Vertex 948 and type=12: $\overline{\tilde{c_{R}}}_{{i_2}}~({p_3})~-\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~- \tilde{c_{R}}_{{i_3}}~({p_4})~-\tilde{c_{L}}_{{i_4}}~({p_2})~$

$$\begin{eqnarray*}& {a_1^{SSSS}}(948)=\displaystyle{sin^{2}{\theta_w}~g^2~i~ \over 9}&{a_2^ {SSSS}}(948)=0\end{eqnarray*}$$

Vertex 1644 and type=11: $\overline{\tilde{u_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{u_{R}}}_{{i_2}}~({p_3})~- \tilde{u_{R}}_{{i_1}}~({p_2})~-\tilde{u_{R}}_{{i_2}}~({p_4})~$

$$\begin{eqnarray*}& {a^{SSSS}}(1644)=\displaystyle{-8~sin^{2}{\theta_w}~g^2~i~ \over 9}\end{eqnarray*}$$

Vertex 1652 and type=11: $\overline{\tilde{u_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{u_{L}}}_{{i_2}}~({p_3})~- \tilde{u_{L}}_{{i_1}}~({p_2})~-\tilde{u_{L}}_{{i_2}}~({p_4})~$

$$\begin{eqnarray*}& {a^{SSSS}}(1652)=\displaystyle{g^2~i~ \over 18}(-4~{\cos (2{\theta_w})} ~-5)\end{eqnarray*}$$

Vertex 1662 and type=11: $\overline{\tilde{s_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{s_{R}}}_{{i_2}}~({p_3})~- \tilde{s_{R}}_{{i_1}}~({p_2})~-\tilde{s_{R}}_{{i_2}}~({p_4})~$

$$\begin{eqnarray*}& {a^{SSSS}}(1662)=\displaystyle{-2~sin^{2}{\theta_w}~g^2~i~ \over 9}\end{eqnarray*}$$

Vertex 1670 and type=11: $\overline{\tilde{s_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{s_{L}}}_{{i_2}}~({p_3})~- \tilde{s_{L}}_{{i_1}}~({p_2})~-\tilde{s_{L}}_{{i_2}}~({p_4})~$

$$\begin{eqnarray*}& {a^{SSSS}}(1670)=\displaystyle{g^2~i~ \over 18}(-4~{\cos (2{\theta_w})} ~-5)\end{eqnarray*}$$

Vertex 1680 and type=11: $\overline{\tilde{d_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{d_{R}}}_{{i_2}}~({p_3})~- \tilde{d_{R}}_{{i_1}}~({p_2})~-\tilde{d_{R}}_{{i_2}}~({p_4})~$

$$\begin{eqnarray*}& {a^{SSSS}}(1680)=\displaystyle{-2~sin^{2}{\theta_w}~g^2~i~ \over 9}\end{eqnarray*}$$

Vertex 1690 and type=11: $\overline{\tilde{d_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{d_{L}}}_{{i_2}}~({p_3})~- \tilde{d_{L}}_{{i_1}}~({p_2})~-\tilde{d_{L}}_{{i_2}}~({p_4})~$

$$\begin{eqnarray*}& {a^{SSSS}}(1690)=\displaystyle{g^2~i~ \over 18}(-4~{\cos (2{\theta_w})} ~-5)\end{eqnarray*}$$

Vertex 1698 and type=11: $\overline{\tilde{c_{R}}}_{{i_1}}~({p_1})~-\overline{\tilde{c_{R}}}_{{i_2}}~({p_3})~- \tilde{c_{R}}_{{i_1}}~({p_2})~-\tilde{c_{R}}_{{i_2}}~({p_4})~$

$$\begin{eqnarray*}& {a^{SSSS}}(1698)=\displaystyle{-8~sin^{2}{\theta_w}~g^2~i~ \over 9}\end{eqnarray*}$$

Vertex 1708 and type=11: $\overline{\tilde{c_{L}}}_{{i_1}}~({p_1})~-\overline{\tilde{c_{L}}}_{{i_2}}~({p_3})~- \tilde{c_{L}}_{{i_1}}~({p_2})~-\tilde{c_{L}}_{{i_2}}~({p_4})~$

$$\begin{eqnarray*}& {a^{SSSS}}(1708)=\displaystyle{g^2~i~ \over 18}(-4~{\cos (2{\theta_w})} ~-5)\end{eqnarray*}$$