squark-squark-G 16 Vertices

There are 16 vertices in the section

Vertex 725 and type=5: $\overline{\tilde{b_{1}}}({p_2})~-\tilde{b_{2}}({p_1})~-G^0({p_3})~$

$$\begin{eqnarray*}& {a^{SSS}}(725)=\displaystyle{g \over 2~ \sqrt{2}~{\cos {\bet... ...{m_{Z}}~A_{b}~{y_{b}}~- \sqrt{2}~{\sin {\beta}} ~{\mu}~{m_{b}}~)\end{eqnarray*}$$

Vertex 726 and type=5: $\overline{\tilde{b_{2}}}({p_2})~-\tilde{b_{1}}({p_1})~-G^0({p_3})~$

$$\begin{eqnarray*}& {a^{SSS}}(726)=\displaystyle{g \over 2~ \sqrt{2}~{\cos {\bet... ...{m_{Z}}~A_{b}~{y_{b}}~+ \sqrt{2}~{\sin {\beta}} ~{\mu}~{m_{b}}~)\end{eqnarray*}$$

Vertex 729 and type=5: $\overline{\tilde{t_{1}}}({p_2})~-G^+({p_3})~-\tilde{b_{1}}({p_1})~$

$$\begin{eqnarray*}& {a^{SSS}}(729)=\displaystyle{g~i~ \over 2~{\sin (2{\beta})} ... ...s {\theta_t}} ~sin^{2}{\beta}~{\sin {\theta_b}} ~ {\mu}~{m_{b}}~)\end{eqnarray*}$$

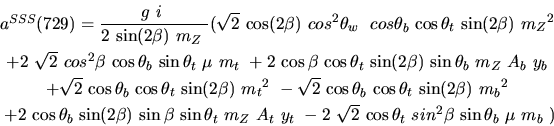
Vertex 730 and type=5: $\overline{\tilde{t_{2}}}({p_2})~-G^+({p_3})~-\tilde{b_{1}}({p_1})~$

$$\begin{eqnarray*}& {a^{SSS}}(730)=\displaystyle{g~i~ \over 2~{\sin (2{\beta})} ... ...{2}{\beta}~{\sin {\theta_b}} ~{\sin {\theta_t}} ~{\mu}~ {m_{b}}~)\end{eqnarray*}$$

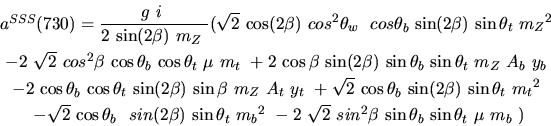
Vertex 733 and type=5: $\overline{\tilde{t_{1}}}({p_2})~-G^+({p_3})~-\tilde{b_{2}}({p_1})~$

$$\begin{eqnarray*}& {a^{SSS}}(733)=\displaystyle{g~i~ \over 2~{\sin (2{\beta})} ... ...} ~{\sin {\theta_b}} ~{\sin {\theta_t}} ~{m_{Z}}~ A_{t}~{y_{t}}~)\end{eqnarray*}$$

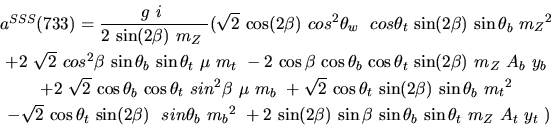
Vertex 734 and type=5: $\overline{\tilde{t_{2}}}({p_2})~-G^+({p_3})~-\tilde{b_{2}}({p_1})~$

$$\begin{eqnarray*}& {a^{SSS}}(734)=\displaystyle{g~i~ \over 2~{\sin (2{\beta})} ... ...n (2{\beta})} ~{\sin {\theta_b}} ~{\sin {\theta_t}} ~{m_{b}}^2~)\end{eqnarray*}$$

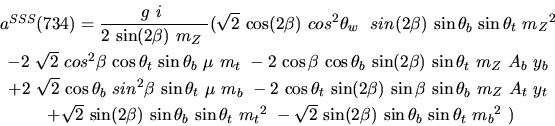
Vertex 737 and type=5: $\overline{\tilde{b_{1}}}({p_2})~-\tilde{t_{1}}({p_1})~-G^-({p_3})~$

$$\begin{eqnarray*}& {a^{SSS}}(737)=\displaystyle{g~i~ \over 2~{\sin (2{\beta})} ... ...s {\theta_t}} ~sin^{2}{\beta}~{\sin {\theta_b}} ~ {\mu}~{m_{b}}~)\end{eqnarray*}$$

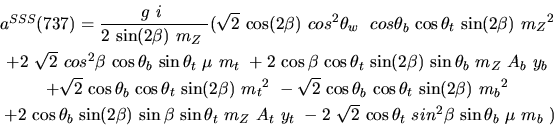
Vertex 738 and type=5: $\overline{\tilde{b_{2}}}({p_2})~-\tilde{t_{1}}({p_1})~-G^-({p_3})~$

$$\begin{eqnarray*}& {a^{SSS}}(738)=\displaystyle{g~i~ \over 2~{\sin (2{\beta})} ... ...} ~{\sin {\theta_b}} ~{\sin {\theta_t}} ~{m_{Z}}~ A_{t}~{y_{t}}~)\end{eqnarray*}$$

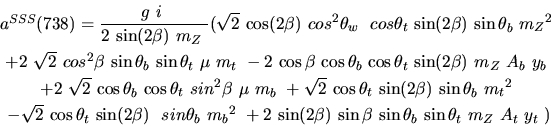
Vertex 739 and type=5: $\overline{\tilde{b_{1}}}({p_2})~-\tilde{t_{2}}({p_1})~-G^-({p_3})~$

$$\begin{eqnarray*}& {a^{SSS}}(739)=\displaystyle{g~i~ \over 2~{\sin (2{\beta})} ... ...{2}{\beta}~{\sin {\theta_b}} ~{\sin {\theta_t}} ~{\mu}~ {m_{b}}~)\end{eqnarray*}$$

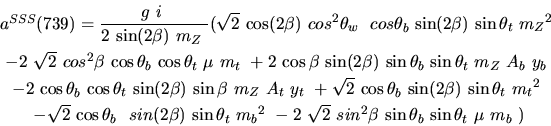
Vertex 740 and type=5: $\overline{\tilde{b_{2}}}({p_2})~-\tilde{t_{2}}({p_1})~-G^-({p_3})~$

$$\begin{eqnarray*}& {a^{SSS}}(740)=\displaystyle{g~i~ \over 2~{\sin (2{\beta})} ... ...n (2{\beta})} ~{\sin {\theta_b}} ~{\sin {\theta_t}} ~{m_{b}}^2~)\end{eqnarray*}$$

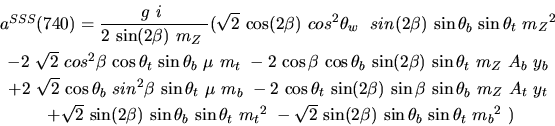
Vertex 753 and type=5: $\overline{\tilde{t_{1}}}({p_2})~-\tilde{t_{2}}({p_1})~-G^0({p_3})~$

$$\begin{eqnarray*}& {a^{SSS}}(753)=\displaystyle{g \over 2~ \sqrt{2}~{\sin {\bet... ...\beta}} ~{\mu}~{m_{t}}~+2~ sin^{2}{\beta}~{m_{Z}}~A_{t}~{y_{t}}~)\end{eqnarray*}$$

Vertex 754 and type=5: $\overline{\tilde{t_{2}}}({p_2})~-\tilde{t_{1}}({p_1})~-G^0({p_3})~$

$$\begin{eqnarray*}& {a^{SSS}}(754)=\displaystyle{g \over 2~ \sqrt{2}~{\sin {\bet... ...\beta}} ~{\mu}~{m_{t}}~-2~ sin^{2}{\beta}~{m_{Z}}~A_{t}~{y_{t}}~)\end{eqnarray*}$$

Vertex 801 and type=5: $\overline{\tilde{c_{L}}}({p_1})~-G^+({p_3})~-\tilde{s_{L}}({p_2})~$

$$\begin{eqnarray*}& {a^{SSS}}(801)=\displaystyle{ \sqrt{2}~{\cos (2{\beta})} ~cos^{2}{\theta_w}~{m_{Z}}~g~i~ \over 2}\end{eqnarray*}$$

Vertex 807 and type=5: $\overline{\tilde{d_{L}}}({p_1})~-\tilde{u_{L}}({p_2})~-G^-({p_3})~$

$$\begin{eqnarray*}& {a^{SSS}}(807)=\displaystyle{ \sqrt{2}~{\cos (2{\beta})} ~cos^{2}{\theta_w}~{m_{Z}}~g~i~ \over 2}\end{eqnarray*}$$

Vertex 811 and type=5: $\overline{\tilde{s_{L}}}({p_1})~-\tilde{c_{L}}({p_2})~-G^-({p_3})~$

$$\begin{eqnarray*}& {a^{SSS}}(811)=\displaystyle{ \sqrt{2}~{\cos (2{\beta})} ~cos^{2}{\theta_w}~{m_{Z}}~g~i~ \over 2}\end{eqnarray*}$$

Vertex 817 and type=5: $\overline{\tilde{u_{L}}}({p_1})~-G^+({p_3})~-\tilde{d_{L}}({p_2})~$

$$\begin{eqnarray*}& {a^{SSS}}(817)=\displaystyle{ \sqrt{2}~{\cos (2{\beta})} ~cos^{2}{\theta_w}~{m_{Z}}~g~i~ \over 2}\end{eqnarray*}$$